Abstrakt
Ovaj rad numerički analizira spregnuti prenos toplote kroz dvostruko zastakljen prozor korištenjem metoda konačnih razlika. Cilj rada je određivanje toplotno optimalne debljine vazdušnog sloja između dve ploče stakla u različitim klimama. Proučavanja su vršena u tri grada koji su predstavljali različite klimatske uslove: ovde su za stakla postavljeni mnogo realističniji granični uslovi nego u [1]. U [1] su stakla smatrana izotermalnim površinama, dok je ovde primenjena analiza spregnutog prenosa toplote. Za spoljne površine okrenute unutra i spolja primenjena su dva granična uslova: konstantna temperatura i konvekcija. Izabrana je visina prozora H od 80 cm i debljina svakog stakla 4 mm. Analizirani su efekti debljine vazdušnog sloja koji varira od 3 do 40 mm prosečnom Nuseltovom broju i toplotnom fluksu kroz ploču stakla. Pokazano je da se energetski gubici kroz dvostruko zastakljene prozore mogu znatno smanjiti optimizacijom debljine vazdušnog sloja. Takođe je pokazano da punjenje prostora između staklenih ploča gasom sa nižom toplotnom provodljivošću umesto vazduhom povećava izolacionu vrednost prozora.
Ključne reči: niska potrošnja energije za zgrade, prozori sa dvostrukim staklima, spregnuti prenos toplote, provodljivost zida, optimalna debljina sloja, numerička simulacija
Oznake
g ubrzanje zemljine teže, m/s²
h konvektivni koeficijent prelaza toplote, W/m²K
H visina otvora za prozor, m
λ koeficijent toplotne provodljivosti vazduha, W/mK
l debljina svake ploče, mm
L debljina vazdušnog sloja između dve ploče, mm
n koordinata u normalnom pravcu
Nu Nusseltov broj
PD procenat smanjenja toplotnog fluksa, f
Pr Prandtlov broj
q toplotni fluks, W/m²
R odnos aspekta (H/L)
Ra Raylergh–ov broj
t vreme, s
T temperatura, K
u komponenta brzine u x–pravcu, m/s
U bezdimenzionalna komponenta brzine u x–pravcu
v komponenta brzine u y–pravcu, m/s
V bezdimenzionalna komponenta brzine u y–pravcu
x,y koordinate definisane na slici 1
X,Y bezdimenzionalne koordinate
Grčke oznake
α toplotna difuzivnost, m²/s
β zapreminski koeficijent toplotnog širenja, 1/K
θ bezdimenzionalna temperatura
ζ bezdimenzionalno vrtloženje
τ bezdimenzionalno vreme
φ generalisana bezdimenzionalna varijabla
ψ bezdimenzionalna strujna funkcija
Znaci
C hladan zid
cr kritično
H topli zid
i,j indeksi koordinata
opt optimum
ref referenca
wal na zidu
x u x pravcu
y u y pravcu
1. UVOD
Zbog porasta energetskih troškova i brige o globalnom očuvanju životne sredine, mnoge zemlje preduzimaju mere da poboljšaju energetsku efikasnost u građevinskom sektoru. U vezi toga, poslednjih godina se sprovode brojne studije koje se tiču zgrada sa niskom potrošnjom energije i odličnim komforom.
Prozori koji obezbeđuju prirodno osvetljenje, ventilaciju i zaštitu od vremenskih uslova pred- stavljaju veoma važne komponenete stambenih i poslovnih zgrada. Međutim, poznato je da prozori kao toplotno najslabija karika u lancu zgrade predstavljaju toplotne rupe. Oni uzrokuju znatan gubitak toplote i termalnu neudobnost zbog veoma loših izolacionih karakteristika, tj. visoke toplotne provodljivosti stakla. Jedan način za smanjenje gubitaka energije kroz prozore je ugradnja dvostruko zastakljenih prozora. Pošto sloj vazduha između dve ploče stakla ima veoma nizak koeficijent provodljivosti toplote, većina energetskih gubitaka zbog grejanja ili klimatizacije kroz prozore se može sprečiti. Popularne su velike zastakljene površine čime se povećava važnost dvostruko zastakljenih prozora. Jedan od najvažnijih aspekata dvostruko zastakljenih pro- zora koji se odnosi na energetsku efikasnost je debljina vazdušnog sloja između dve staklene ploče. On ima značajan efekat na gubitke energije kroz prozore. Za tu vrednost se mora definisati optimalna vrednost koja energetske gubitke smanjuje na minimum. Neki parametri poput unutrašnje i spoljašnje temperature, vremenskih uslova, klime itd. utiču na optimalnu vrednost debljine vazudšnog sloja. Iz tog razloga će predviđanje optimalne vrednosti za različite oblasti, što je i cilj ovog rada, pomoći ekonomiji i očuvati smanjenje potrošnje energije.
U interesantnoj numeričkoj studiji koja je usko povezana sa njihovim radom, Korpela i saradnici [2] su istraživali prenos toplote kroz dvostruko zastakljeni prozor. Kada su Rayleigh broj i aspekt otvora imali visoke vrednosti napravljen je opis višećelijskog konvekcijskog toka. Korištenjem Arakavine eksplicitne šeme konačnih razlika za konvektivne uslove i eksplicitne Dufort–Frankel metode za uslove difuzije, odredili su granice između provodljivog, višećelijskog i prelaznog režima toka u otvor za prozor za R ≤ 20. Kasnije su Lee i Korpela [3] predstavili opštije numeričke rezultate koji važe za odnos aspekta otvora R ≤ 40 i za različite Prandtlove brojeve. Prenos toplote prirodnom konvekcijom za otvor dvostruko zastakljenog prozora teoretski su ispitivali Novak i Nowak [4] korištenjem metode konačnih razlika. Oni su procenjivali različite granične režime toka fluida za odnose aspekta otvora 10 ≤ R ≤ 90 i za oblast Grashofovih brojeva 1 x 108 ≤ Gr ≤ 3 x 109. Zhang i ostali [5] su istraživali efekat toplotne izolacije zastora ugrađenog unutar dvostruko zastakljenog prozora. Zastor je bio venecijaner od horizontalnih lamela koje su se mogle rotirati. Oni su numerički odredili efekat propustljivog zastora na polje temperature, toka i na ukupni prenos toplote. Medved i Novak [6] su istraživali prenos toplote kroz dvostruko zastakljen prozor sa zastorom i sifonom koji su formirali poluotvorenu šupljinu pomoću PHOENICS komercijalnog CFD paketa. Muneer i Han [7] su predstavili analizu za izračunavanje konvektivnog prenosa toplote dvostruko zastakljenog prozora. Prikazan je i potencijal za veliku uštedu energije upotrebom teških inertnih gasova poput kriptona i ksenona.
Abodahab i Muneer [8] su koristili tehnike merenja i modeliranja u cilju promene temperature, po dužini, dvostruko zastakljenih prozora. Oni su obezbedili fizički model koji se može koristiti za izračunavanje temperatura po visini dvostruko zastakljenih prozora. U drugoj njihovoj studiji [9] uveli su model za izračunavanje promena noćne temperature, pod uslovom da je poznata spoljna temperatura. Razvijen je softver baziran na tabelama za određivanje učestalosti kondenzacije koja se može javiti na nekom dvostruko zastakljenom prozoru. Weir i Muneer [10] su izvršili kvalifikaciju ostvarene energije četiri glavna materijala korištena za pravljenje dvostruko zastakljenih prozora datih dimenzija, sa inertnim gasom između staklenih ploča. Četiri glavna materijala koja su uzeta u obzir su bila gas (argon, kripton i ksenon), drvo, aluminijum i staklo.
Procenjivane su i energetske potrebe proizvodnog procesa. Sekhar i Toon [11] su napravili studiju o dobrim osobinama „pametnog“ prozora, dvostruko zastakljene jedinice čija je jedna ploča visoko kvalitetno toplotno reflektujuće staklo, a druga je prevučena nisko emisionom prevlakom. Opisan je njen postignuti uticaj na loše hlađenje, potrošnju energije i uštedu energije u poređenju sa ostalim oblicima zastak- ljivanja. Analizirani su i troškovi života i smanjenje atmosferskih zagađivača. Gavin i Willson [12] su predstavili privremene vrednosti rezultata u eksperimentu koji je pratio uslove okruženja otvora za zastakljivanje brojnih tipova prozorskih ramova. Merenje relativne vlažnosti, temperature i prisustvo vlage u tečnom stanju u otvorima oko ivica dvostruko zastakljenih jedinica vršena su tokom dvogodišnjeg perioda posmatranja.
Aydin [1] je posmatrao prenos toplote kroz dvostruko zastakljen prozor, da bi odredio termalno optimalnu debljinu vazdušnog sloja između dve staklene ploče, u različitim klimama. Otkriveno je da se gubici energije kroz dvostruko zastakljene prozore mogu znatno smanjiti optimizacijom debljine vazdušnog sloja. Za svaku površinu stakla pretpostavljene su konstantne temperature, zanemarujući provodljivost ploča. Ova studija je nastavak reference [1] koja uzima u obzir provodljivost stakla. Za spoljne površine steklenih ploča korištena su dva različita uslova termalnih ograničenja: konstantna temperatura i fluks konvekcije. U prvom slučaju, temperature spoljnih površina obe staklene ploče su uzete kao konstanta koja je jednaka unutrašnjim i spoljašnjim temperaturama zimi, pojedinačno. U drugom slučaju za spoljne površine stakla definisan je uslov konvekcije. Za predstavljanje različitih klima u Srbiji i Crnoj Gori uzeta su tri grada. Za svaki grad je određena optimalna debljina vazdušnog sloja između dve staklene ploče korištenjem metoda konačnih razlika, da bi se energetski gubici kroz dvostruko zastakljene prozore smanjili na minimum.
U većini studija iz literature zanemarena je interakcija između konvekcije unutra i provodljivosti u zidovima. U referenci [13] date su neke studije u kojima se proučava spregnuta konvekcija u prostoru. Meyer i drugi [13] su proučavali efekte debljine zida jedinice i toplotne provodljivosti na prirodni konvektivni prenos toplote u nagnutim prostorima.
Kim i Visakanta [14] su proučavali efekte provodljivosti zidova na prirodnu konvekciju u različito orijentisanim četvrtastim otvorima.
Prikazana je provodljivost toplote veznih (nezagrevanih) zidova, da bi se istovremeno stabilizovao i destabilizovao fluid u otvoru. Kaminski i Prakash [15] su proučavali spregnutu prirodnu konvekciju u četvrtastom otvoru čija je jedna vertikala bila debela sa konačnom toplotnom provodljivošću, dok su ostala tri zida imala debljinu nula.
Oni su ispitivali tri posebna modela u vezi provodljivosti zidova: (i) kompletan spregnuti slučaj u kojem je pretpostavljena potpuno dvodimenzionalna provodljivost u debeloj vertikali, (ii) jednodimenzionalni model u kojem je pretpostavljena provodljivost samo u horizontalnom pravcu, (iii) ukupan pristup parametrima koji pretpostavlja ujednačenu temperaturu dodirne površine čvrstog materijala i fluida. Mallinson [16] je opisao numerički model za interakciju između prirodne konvekcije u otvoru i provodljivosti bočnih zidova koji su paralelni u odnosu na ravan otvora. Prikazani su savršeno provodljivi zidovi, da bi se smanjio stepen prenosa toplote fluidom i da se poveća jačina toka. Zimmerman i Acharya [17] su napravili numerički studiju prirodne konvekcije u otvoru sa savršeno provodljivim horizontalnim spoljnim zidovima i konačno provodljivim pregradnim zidovima. Le Putrec i Lauriat [18] su analizirali efekte toplotnih gubitaka na provodljivim stranama zidova za 3–D prirodnu kovekciju u pravougaonim otvorima. Heindel [19] i drugi su proučavali vezani transport provodljivosti i prirodne konvekcije u 2–D i 3–D malo zagrevanim otvorima. Sun i Emery [20] su ispitivali prenos toplote spregnute prirodne konvekcije u 2–D vazduhom napunjenog prostora koji ima male unutrašnje izvore toplote i unutrašnju pregradu. Kimura i drugi [21] su analitički i eksperimentalno istraživali prenos toplote pri spregnutoj prirodnoj konvekciji sa vertikalne ploče za koju su korištena tri različita materijala koja uključuju bakar, nerđajući čelik i keramiku. Baytas [22] i ostali su numerički proučavali konstantno stanje spregnute prirodne konvekcije u kvadratnom otvoru napunjenom poroznim sredstvom i pokazali su da sa porastom odnosa provodljivosti čvrsta materija – fluid opadaju prosečne vrednosti Nuseltovog broja duž vertikalnih toplih i hladnih zidova. Liaqat i Baytas [23] su proučavali spregnutu prirodnu konvekciju u četvrtastom otvoru koji sadrži zapreminske otvore.
2. Matematička formulacija i numerički metod
Tok i prenos energije u dvostruko zastakljenim prozorima je važan primer prenosa toplote prirodnom konvekcijom u prostoru. Na slici 1 je prikazana konfiguracija, naznačeni su otvor prozora dužine L i visine H u Dekartovim koordinatama sa odgovarajućim komponentama brzine (u, v) kao što je ranije objašnjeno, u ovoj studiji su razmatrana provodljivost staklenih ploča (spregnute analize). Određeno je da debljine svih ploča l budu jednake. Određen je fluid koji se ne može sabijati, sa konstantnim osobinama, mada su efekti uzgona razmatrani pozivajući se na Busineskove aproksimativnosti. U jednačini za energiju zanemareni su rad kompresije i viskoznog rasipanja. U odnosu na konvekciju je zanemareno toplotno zračenje. Uz prethodne pretpostavke, glavne jednačine za razmatrani dvodimenzionalni tok su prvo pisane pomoću primitivnih varijabli. Eliminacijom pritiska dobijene su jednačine u funkciji bezdimenzionalne strujne funkcije i vrtloženja koji su respektivno predstavljeni na sledeći način.
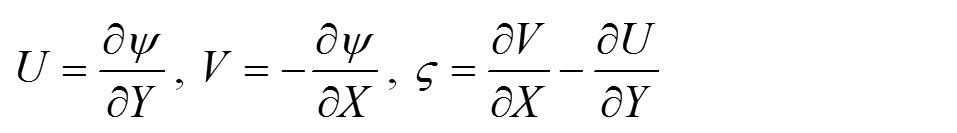
Otuda je uobičajena formulacija vrtložno – strujne funkcije za problem u bezdimenzionalnom obliku predstavljena na sledeći način.
Jednačine strujne funkcije

Jednačina transporta vrtloga
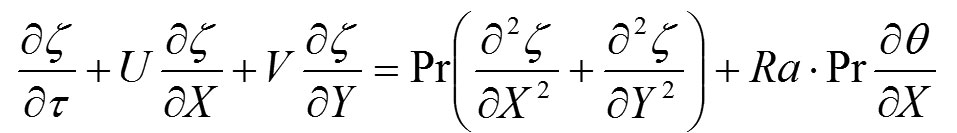
Jednačina energije
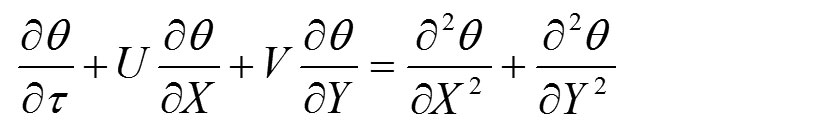
Ove jednačine su bezdimenzionalne zbog korišćenja visine H kao dužne skale i definisanja promenljivih na sledeći način
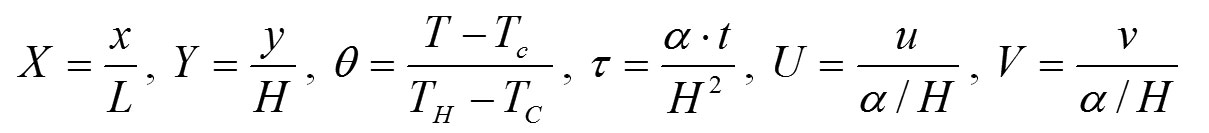
U gore navedenim jednačinama je Prandtlov broj, a Ra je Rayleigh broj definisan na sledeći način
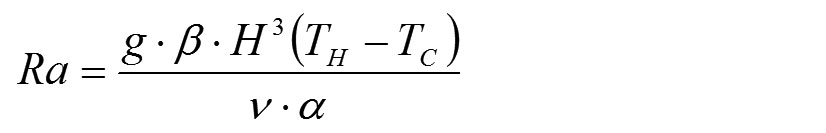
Pošto je prostor prozora veoma visok, provođenje u vertikalnom pravcu je zanemareno razmatrajući jednodimenzionalno provođenje zida. Na dodirnoj površini čvrste materije i fluida temperatura i toplotni fluks moraju biti kontinuirani. To se tretira kao:
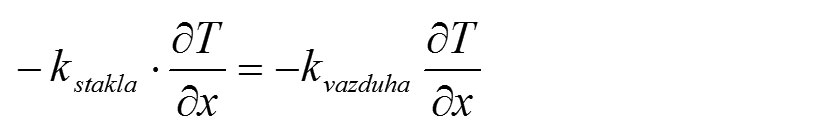
U bezdimenzionalnom obliku, gore napisana jednačina se može napisati kao
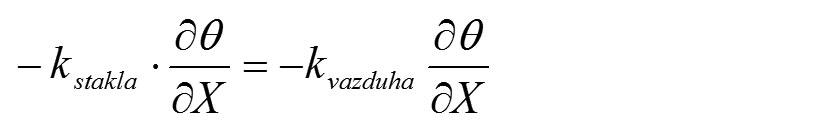
Korišćenje jednodimenzionalnog pristupa za provodljivost svake staklene ploče predstavlja veliku prednost pošto nije potrebno rešavati jednačine za toplotnu provodljivost zida, tj. potrebno je rešiti samo jednačine toka, a efekat provodljivosti zida se primenjuje kroz granične uslove izražene u gornjoj jednačini gde je x = 0, x = 1.
To omogućava znatne uštede u računanju.
Ako se uzme granični fluks konvekcije za spoljne površine staklenih ploča, fluks na spoljnim površinama se može napisati kao
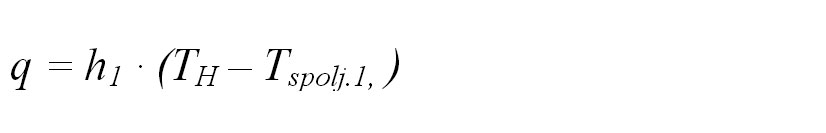
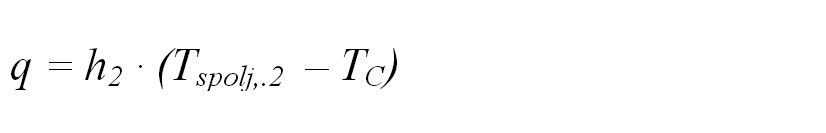
gde su h1 i h2 koeficijenti prelaza toplote za unutrašnje i spoljašnje prostore kojima je prozor okrenut, a TH i TC su temperature ovih prostora. Tspoljni,1 i Tspoljni,2 su temperature spoljnih površina unutrašnje i spoljašnje staklene ploče (pogledati sliku 1).
Preostali usvojeni granični uslovi su
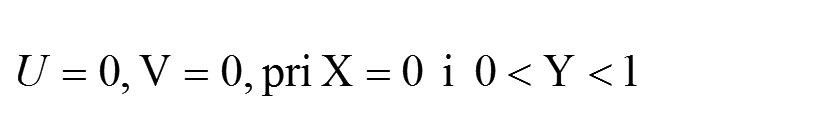
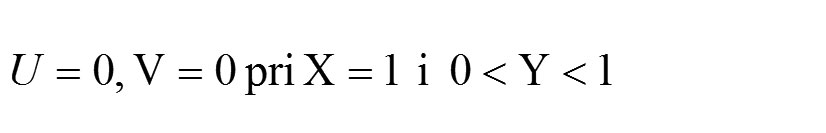
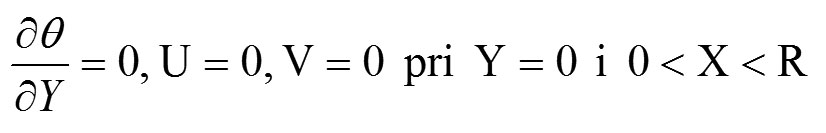
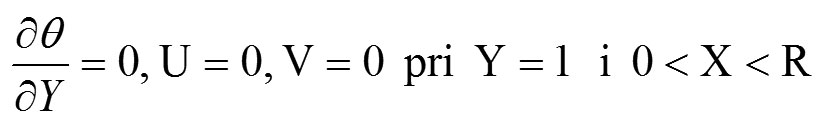
gde R = H/L karakteriše otvor prozora
Stacionarni uslovi u zidu gde ne postoji fluks mase duž neke čvrste granice vodi ka uslovu
. Otuda na granicama otvora (vezano za rastojanje između ploča) je proizvoljno specifikovan kao nula. Vrednost vrtloga na granici je računat pomoću šeme sa tri uzastopne tačke za strujnu funkciju.
Ova relacija donosi:
gde je vrednost vrtloženja na zidu i n je spoljna normala površine.
U numeričkim proračunima vrednost vrtloga na uglovima je uzeta kao prosečna vrednost u dva susedna čvora. Sa inženjerske tačke gledišta, najvažnija stavka je prenos toplote kroz dvostruko zastakljen prozor. To je najbolje predstavljeno Nusseltovim brojem, koji je mera odnosa prenosa toplote provođenjem i ukupnog prenosa toplote. Prosečni Nusseltov broj za zagrejan zid izražen je pomoću
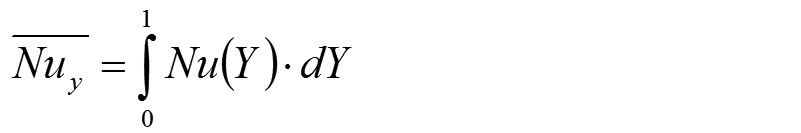
gde je Nu(Y) lokalni Nuseltov broj za zagrejan zid i predstavljen je pomoću sledećeg izraza
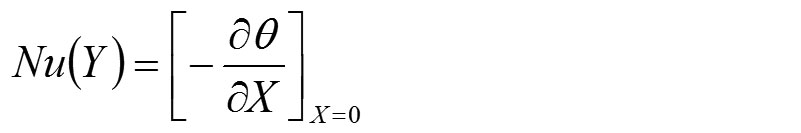
Fluks kroz dvostruko zastakljeni prozor definisan je na sledeći način za oba toplotna granična uslova koji se koriste za spoljne površine staklenih ploča
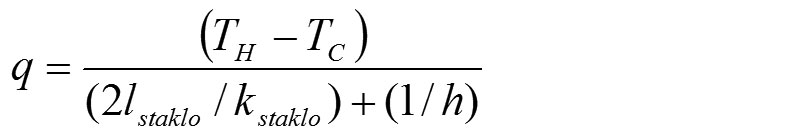
i za slučaj konvekcije je
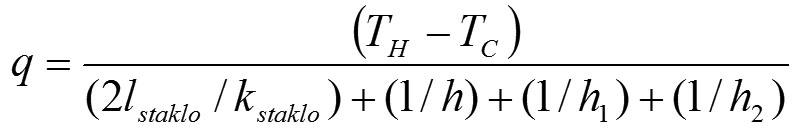
gde je h koeficijent prelaza toplote i dobija se iz
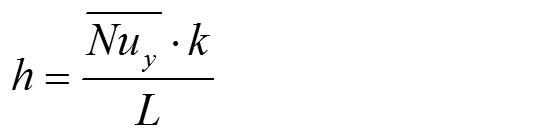
U referenci [1] mogu se naći detalji o metodi numeričke simulacije i vrednosti razvijenog komjuterskog programa.
3. Rezultati i diskusija
Cilj ove studije je određivanje optimalne debljine vazdušnog sloja između dve ploče dvostruko zastakljenih prozora za gradove sa različitim klimatskim uslovima. Gradovi u kojima su vršena ispitivanja su Ivanjica, Beograd i Bar.
U tabeli 1 prikazane su odgovarajuće zimske temperature za ove gradove.
Izabrana je visina prozora od 80 cm, što je jedna od najviše korišćenih vrednosti pri dizajniranju prozora. Uzeta je unutrašnja temperatura od 21ºC, a kao što je ranije navedeno ova studija je nastavak reference [1] gde su pretpostavljene dve izotermske staklene ploče. Ovde je napravljen mnogo realističniji pristup, spregnuta analiza je napravljena uzimajući u obzir provodljivost staklenih ploča. Za spoljne površine staklenih ploča koje su okrenute ka unutrašnjoj i spoljašnjoj strani posebno su primenjena dva različita granična uslova: konstantna temperatura i konvektivni fluks.
Tabela 1
Zimske projektne temperature za gradove razmatrane u ovoj studiji
Tabela 2

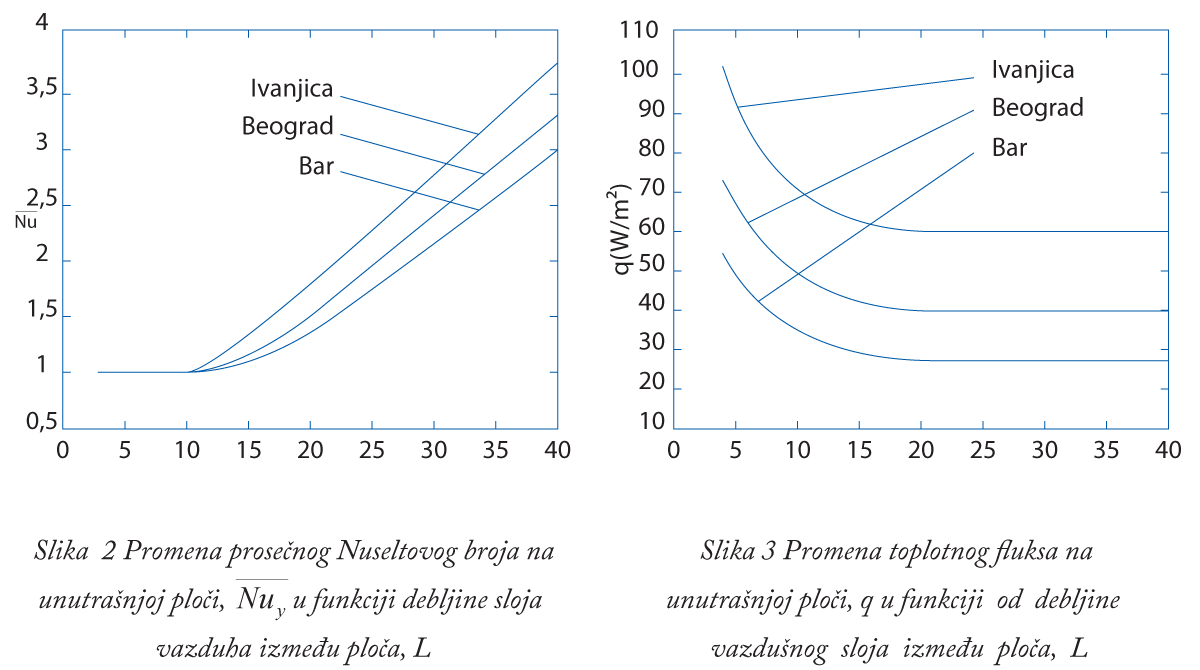
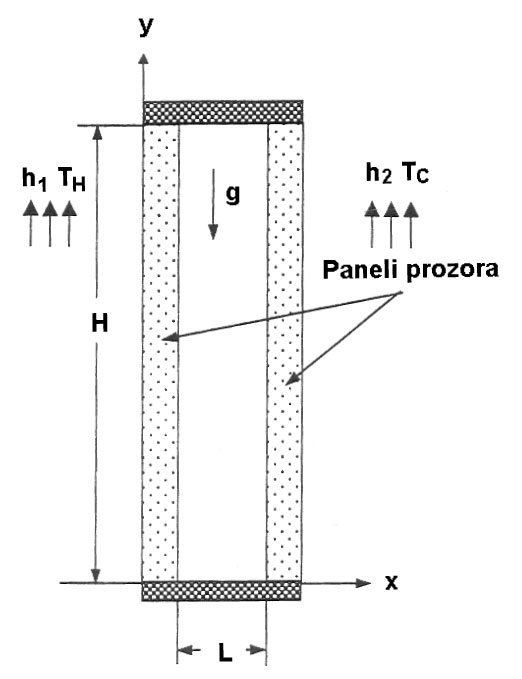
Kada je mehanizam prenosa toplote provodljivošću, prenos toplote rapidno opada sa porastom debljine vazdušnog sloja. Pošto je koeficijent toplotne provodljivosti vazduha nizak, vazdušni sloj se ponaša kao izolacioni materijal. Za veće vrednosti L, konvekcioni mehanizam prenosa toplote počinje da pokazuje svoje efekte u prenosu energije. Za opseg L 10 – 15 mm nastavlja se trend opadanja q sa porastom L, ali sa manjim nagibom. Za ovaj opseg L mogu se porediti mehanizmi provođenja i konvekcije.
Iz tog razloga je opadanje prenosa toplote sa porastom L usled provođenja izbalansirano sa porastom prenosa toplote usled prirodne konvekcije u zatvorenom sloju vazduha. Za vrednosti veće od L = 15 mm, efekat debljine vazdušnog sloja na fluks varira od grada do grada. Kao što se može videti za Bar, porast toplotnog fluksa se neznatno nastavlja do 21 mm.
To nastaje usled uporedivih efekata mehanizama provođenja i konvekcije. Za vrednosti iznad L = 21 mm, q raste sa porastom L, zbog činejnice da konvekcija dominira nad provodljivošću. Stoga je izbor rastojanja između dve staklene ploče u opsegu 18 – 21 mm optimalno rešenje za Bar. Odgovarajući opseg za Beograd je 15 – 18 mm, dok je za Ivanjicu 12 – 15 mm.
Ovi rezultati su slični rezultatima iz reference [1]. Ovde su, u odnosu na vrednosti iz reference [1] dobijene niže vrednosti i za i q zbog uzimanja u obzir provođenja.
Provodljivost u svakoj staklenoj ploči formira otpornost na prenos toplote i, shodno tome, smanjuje prenos toplote. Upotrebom optimalne vrednosti debljine vazdušnog sloja može se izračunati procenat opadanja toplotnog fluksa
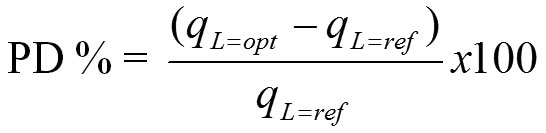
gde qL=opt i qL=ref predstavljaju toplotne fluksove pri optimalnoj i referentnoj vrednosti debljine vazdušnog sloja. Ako se ovde dobijene optimalne vrednosti koriste umesto
L = 9 mm koje se pre često koristilo za projektovanje prozora, dobiće se sledeća ušteda energije: 27 % za Bar, 23 % za Beograd i 19 % za Ivanjicu.
Gore pomenute vrednosti dobijene spregnutom analizom su znatno niže od vrednosti dobijenih u referenci [1], gde su zanemareni efekti provodljivosti staklenih ploča i gde su ploče smatrane izotermskim površinama.
Kao što je i očekivano, korištenje fluida sa nižom provodljivošću dovešće do smanjenih vrednosti prenosa toplote od vrednosti za vazduh. To se postiže zbog sledeća dva efekta niže provodljivosti: (1) otpornost provođenju u staklenoj ploči će porasti, (2) niža provodljivost će smanjiti unutrašnju temperaturu staklo paketa.
Ove smanjene unutrašnje temperature će posledično smanjiti keoficijent prelaza toplote prirodnom konvekcijom, smanjujući silu potiska u fluidu.
Ovde je, kao primer, izabran gas sa toplotnom provodljivošću od 15 • 10–3 W/mK. Za Bar je prijavljeno da debljina vazdušnog sloja od 9 mm između dve staklene ploče predstavlja toplotno optimalno rešenje. Pokazano je da sloj fluida korišten umesto vazduha, debljine 21 mm, koji ima toplotnu provodljivost od 15 • 10–3 W/mK, može da ostvari uštedu energije od 40 % u odnosu na vazduh.
Slučaj 2: Stanje konvekcionog fluida za spoljne površine staklenih ploča
Kao što je ranije prikazano, h2 predstavlja koeficijent prelaza toplote za spoljni prostor a ispitan je njegov efekat na prenos toplote.kao što je dobro poznato, klima, vetrovitost itd. u nekoj oblasti imaju važan uticaj na prenos toplote od spoljnog vazduha do staklene ploče. U zavisnosti od jačine vetra, menja se prinudni koeficijent prelaza toplote. U ovoj studiji za vrednosti konvektivnog prelaza toplote zida izabrana su četiri različite vrednosti: 15, 20, 25 i 30 W/m²K.
Pretpostavljena konvekcija za spoljne površine staklenih ploča vodi do manjih vrednosti prenos atoplote od onih sa pretpostavljenim konstantnim temperaturama, slučaj 1. To je zbog činjenice da pri pretpostavci konstantne temperature za spoljne površine zanemarujemo konvektivni otpor unutrašnjeg i spoljašnjeg vazduha prenosu toplote. Uzimanje u obzir ovih otpora će, normalno, dovesti do smanjenih vrednosti prenosa toplote, kao što je i očekivano.
Sa praktične tačke gledišta, cilj nam je bio toplotna optimizacija debljine vazdušnog sloja između staklenih ploča prozora. Oba uslova za spoljne površine staklenih ploča rezultuju istom toplotno optimalnom debljinom vazdušnog sloja za bilo koji razmatrani region. Iz tog razloga se rezultati dobijeni u slučaju 1 gde su se koristile pretpostavke konstantne temperature za spoljne površine staklenih ploča mogu generalizovati.
U skladu sa ranije navedenim, napravljen je drugi pokušaj određivanja vrednosti efekta prinudnog koeficijenta prelaza toplote spoljne površine staklene ploče h2. Zbog dužine članka, predstavljeni su samo rezultati za Beograd za debljinu vazdušnog sloja od 21 mm: porast koeficijenta prelaza toplote kod prinudne konvekcije h2 od 15 do 30 W/m²K nije puno uticao, samo 2,6% porasta. Gore navedeni nalazi potvrđuju vrednost rezultata dobijenih u slučaju 1 za svaku oblast, od manje vetrovite do dosta vetrovite.
Konačno, potrebno je setiti se da je ovde naš cilj bio dobijanje toplotno optimalne debljine vazdušnog sloja. U nekim drugim slučajevima, npr. ako je cilj kontrola emitovanja zvuka, dobili bi se različiti rezultati u poređenju sa toplotnim tokom.
4. Zaključci
U ovoj studiji je izvedena analiza prenosa toplote kroz dvostruko zastakljeni prozor. U fokusu je bilo određivanje optimalne debljine sloja vazduha zarobljenog između staklenih ploča prozora. to je postignuto teoretskim ispitivanjem spregnutog prenosa toplote provođenjem i prirodnom konvekcijom za dvostruko zastakljene prozore, korištenjem metoda konačnih razlika. Za spoljašnje površine stakla su definisana dva različita toplotna granična uslova: konstantna temperatura (slučaj 1) i konvekcioni toplotni fluks (slučaj 2). Ispitivana su tri grada u Srbiji i Crnoj Gori, koji su predstavnici različitih klimatskih uslova, Bar, Beograd i Ivanjica. Na osnovu rezultata iz slučaja 1, oblast optimalne debljine bila je za Bar 18 – 21 mm, za Beograd 15 – 18 mm, za Ivanjicu 12 – 15 mm. Pokazano je da se pri korištenju optimalnih vrednosti mogu dobiti značajne uštede u gubicima energije kroz dvostruko zastakljene prozore. U slučaju 1 je takođe otkriveno da korištenje fluida sa nižom toplotnom provodljivošću povećava izolacione karakteristike dvostruko zastakljenih prozora i smanjuje količinu razmenjene toplote. U slučaju 2 je otkriveno da korištenje uslova konvekcionog fluksa za spoljne površine stvara niže vrednosti rezultata nego za slučajeve u kojima je primenjivan pristup konstantne temperature. To je uzrokovano uglavnom dodatnim unutrašnjim i spoljašnjim otporima prenosu toplote, pošto je pretpostavljeno da su ovi otpori jednaki nuli za uslove konstantnih temperatura za spoljne staklene površine, a pretpostavljen je beskonačni koeficijent prelaza toplote. Takođe je pokazano da povećanje prinudnog koeficijenta prelaza toplote za spoljnu površinu spoljne staklene ploče nije imalo bitnog uticaja na prenos toplote.
Literatura
[1] Aydin O. Determination of optimum air–layer thickness in double–pane windows, Energy and Buildings 2000;32:303–8.
[2] Korpela SA, Lee Y., Drummond JE.; Heat transfer through double pane window, Journal of Heat Transfer 1982;104:539–44.
[3] Lee Y., Korpela SA., Multicellular convection in a vertical slot. Journal of Fluid Mechanics 1983;126:91–121
[4] Novak MH, Nowak ES.; Natural convection heat transfer in slender window cavities, Journal of Heat Transfer 1993;115:476–9.
[5] Zhang Z., Bejan A., Lage JLK.; Natural convection in a certical enclousure with internal permeable screen open at the top. Energy Buildings 1991;113:377–83.
[6] Medved S., Novak P.; Heat transfer thrpugh a double pane window with an insulation screen open at the top. Energy Buildings 1998;28:257–68.
[7] Muneer T. Han B.; Simplified anallysis for free convection in enclosures application to an industrial problem. Energy Conversion and Management 1996;37:1463–7.
[8] Abodahab N., Muneer T.; Free convection analysis of a window cavity and its longitudinal temperature profile. Energy conversion and Management 1998;39: 257–67.
[9] Muneer T., Abodahab N.; Frequency of condensation ocurrence on double glazing in the United Kingdom. Energy Conversion and Management 1998;39:717–26.
[10] Weir G., Muneer T. Energy and environmental impact analysis of double – glazed windows. Energy Conversion and Management 1998; 39: 243–56.
[11] Sekhar Sc. Toon KLC.; On the study of energy performance and life cycle cost of smart window, Energy Buildings 1998;28:307–16.
[12] Garvin SL, Wilson J.; Environmental conditions in window frames with double– glazing units Construction Building Materials 1998;12:289–302.
[13] Meyer BA, Mitchell JW, El – Wakil MM.; The effect of thermal wall properties on natural convection in inclined rectangular cells, Journal of Heat Transfer 1982; 104:111–7.
[14] Kim DM, Viskanta R.; Study of the effects of wall condustance on natural convestion in differently oriented square cavities, Journal of Fluid Mechanics 1984; 144:153–76.
[15] Kaminski DA, Prakash C.; Conjugate natural convection in a square enclousure: effect of conduction in one of the vertical walls, International Journal of Heat and Mass Transfer 1988;29:1979–88.
[16] Mallinson GD.; The effects of side – wall conduction on natural convstion in a slot. Journal of Heat Transfer 1987;109:419–26.
[17] Zimmerman E, Acharya S.; Free convection heat transfer in a partially divided vertical enclosure with conducting end walls. International Journal of Heat and Mass Transfer 1987;30:319–31.
[18] Le Peutrec Y, Lauriat G.; Effect of the heat transfer at the side walls on natural convection in cavites. Journal of Heat Transfer 1990;112:370–8.
[19] Heindel TJ. Incropera FP, Ramadhyani S. Conjugate natural convection from an array of discrete heat sources: part 1–two–and–thre–dimensional model validation. International Journal of Heat and Fluid Flow 1995;16:501–10.
[20] Sun YS, Emery AF, Effects of wall conduction, internal heat and an internal baffle on natural convection heat transfer in a rectangular enclosures. International journal of Heat and Mass Transfer 1997;40:915–29.
[21] Kimura S, Okajima A, Kiwata T. Conjugate natural convestion from a vertical heated slab. International Journal of Heat and Mass transfer 1998;41:3203–11.
[22] Baytas AC, Liaqat A, Grosan T, Pop I. Conjugate natural convection in a square porous cavity. Heat and Mass Transfer 2001;37:467–73.
[23] Liaqat A, Baytas AC. Conjugate natural convection in a square enclosure containing volumetric sources. International Journal of Heat and Mass Transfer 2001;44: 3273–80.
Piše: Prof. dr Dragan Škobalj, Mr Ivan Nikolić, dipl. inž.